Tail Recursion

Hello everyone! 👋

Today’s article will be about tail recursion, a technique that allows you to optimize certain recursive functions.

Introduction

In short, when you write a recursive function, each new call it does allocates a frame onto the stack. For example, let us take this following function:

        private static long RecursiveFib(long n)
        {
            if (n <= 1)
            {
                return n;
            }
            return RecursiveFib(n - 1) + RecursiveFib(n - 2);
        }

If we set a breakpoint at return n and call the function with RecursiveFib(10), we will get the following stack frame. There are 10 entries in the stack frame.

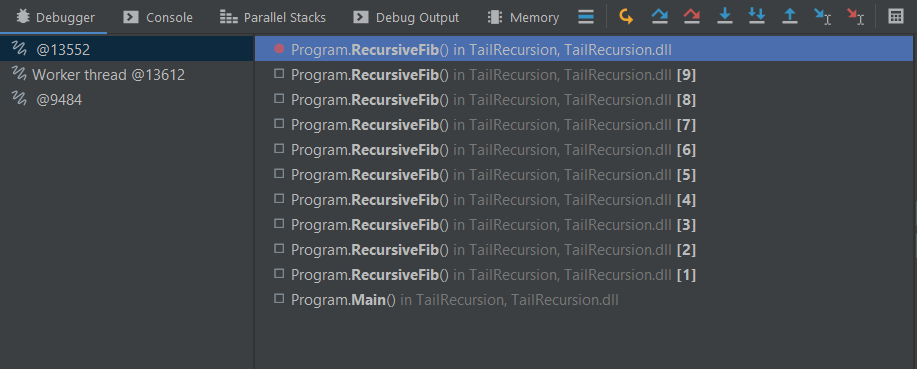Each recursive call to RecursiveFib() is dependent on the previous one and the program needs to add a new stack frame to remember the old calls. The process of adding a new stack frame takes some time, and if your program requires many of them, you may encounter a Stack Overflow error.

If we benchmark RecursiveFib(40) we get an approximation 4986853 elapsed ticks.

Iterative Version

You can rewrite the function in an iterative manner by using a loop and sometimes a stack. Loops can then be further optimized by the compiler by using a technique called Loop Unrolling.

The iterative version of RecursiveFib looks like the following.

        private static long IterativeFib(long n)
        {
            var a = 0L;
            var b = 1L;
            if (n == 0)
            {
                return a;
            }
            for (var i = 1; i < n; i++)
            {
                var c = a + b;
                a = b;
                b = c;
            }

            return b;
        }

In the iterative version the stack of IterativeFib(10) only has 2 entries.

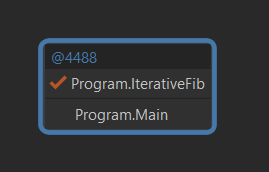The benchmark for IterativeFib(100) shows 19 elapsed ticks, this is ~26246594% faster than the recursive version RecursiveFib(40), and we will not get any stack overflow errors.

Tail Recursion

Tail recursion is just like recursion but instead of using the stack, the compiler will use registers. It is accomplished by writing the function in such a way that the recursive call does not depends on the previous call. You will usually need to add additional parameters to the function’s signature to hold your data.

        private static long TailRecursiveFib(long n, long a , long b )
        {
            return n switch
            {
                0 => a,
                1 => b,
                _ => TailRecursiveFib(n - 1, b, a + b)
            };
        }

The benchmark for TailRecursiveFib(100, 0 ,1) shows 21 elapsed ticks, which is very close to the iterative version.

Conclusion

Tail recursion is a technique of rewriting a recursive function in such a way that the new recursive call will replace the current stack frame, it will not add a new one.

Thanks for reading and I hope you have learned something! 🍻

Full Code Snippet

using System;
using System.Diagnostics;

namespace TailRecursion
{
    static class Program
    {
        private static long TailRecursiveFib(long n, long a , long b )
        {
            return n switch
            {
                0 => a,
                1 => b,
                _ => TailRecursiveFib(n - 1, b, a + b)
            };
        }
        
        private static long RecursiveFib(long n)
        {
            if (n <= 1)
            {
                return n;
            }
            return RecursiveFib(n - 1) + RecursiveFib(n - 2);
        }

        private static long IterativeFib(long n)
        {
            var a = 0L;
            var b = 1L;
            if (n == 0)
            {
                return a;
            }
            for (var i = 1; i < n; i++)
            {
                var c = a + b;
                a = b;
                b = c;
            }

            return b;
        }

        private static void Main(string[] args)
        {
            var st = new Stopwatch();
            var r = new Random();
            for (var i = 0; i < 5; i++)
            {
                RecursiveFib(i);
                IterativeFib(i * 10 );
                TailRecursiveFib(i * 10, 0, 1);
            }

            long result = 0;
            st.Restart();
            // result = RecursiveFib(10);
            result = TailRecursiveFib(100, 0, 1);
            // result = IterativeFib(100);
            st.Stop();
            Console.WriteLine("Elapsed ticks: {0}", st.ElapsedTicks);
            Console.WriteLine(result);
        }
    }
}